On going research topic
2. 기기 구조 설계의 건전성을 판단하기 위하여 ASME 코드의 검증 절차를 자동화합니다.
3. 고차원 뉴럴넷 함수를 활용하여 원자 단위 스케일에서 시뮬레이션한 응력 해석 결과를 연속체 모델로 확대하는 이론적 방법에 대해 연구합니다. [Collaboration with Prof. Nikhil Admal (University of Illinois at Urbana Champaign) and Prof. Ellad Tadmor (Unversity of Minnesota)]
4. 플라즈마 기반 반도체 공정을 기계학습으로 예측하여 실시간 모니터링을 수행하고 공정의 개선 방향을 탐색합니다. [Collaboration with Dr. Hyeong-U Kim (KIMM)]
Machine Learning Based Plasma Process Diagnoistic
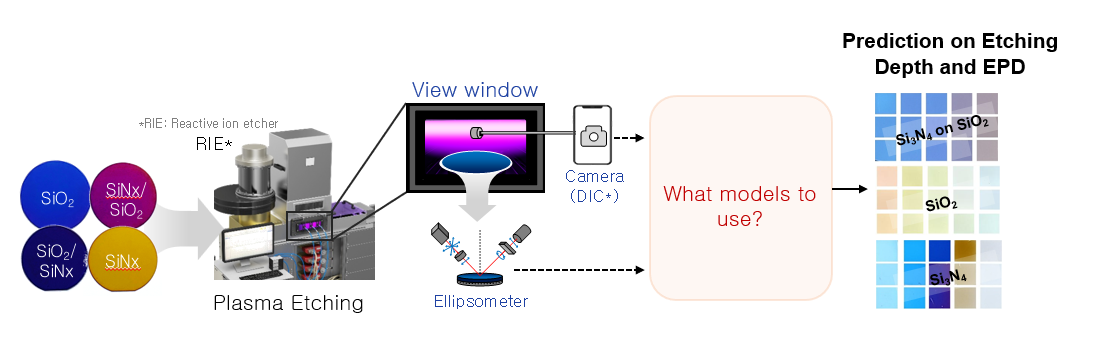
We conduct research on machine learning (ML)-based diagnostics for plasma semiconductor manufacturing processes. Our work focuses on developing real-time, non-contact methods to predict etch depth and insulating layer thickness during plasma etching. By leveraging process parameters or digital image colorimetry (DIC) data as inputs, I apply a range of ML techniques, including neural networks and ensemble models, to improve prediction accuracy and enhance reliability through uncertainty quantification. This approach offers a fast, contamination-free alternative to conventional analysis methods, contributing to improved process stability and manufacturing efficiency.
Fast Marching Based Path Planning
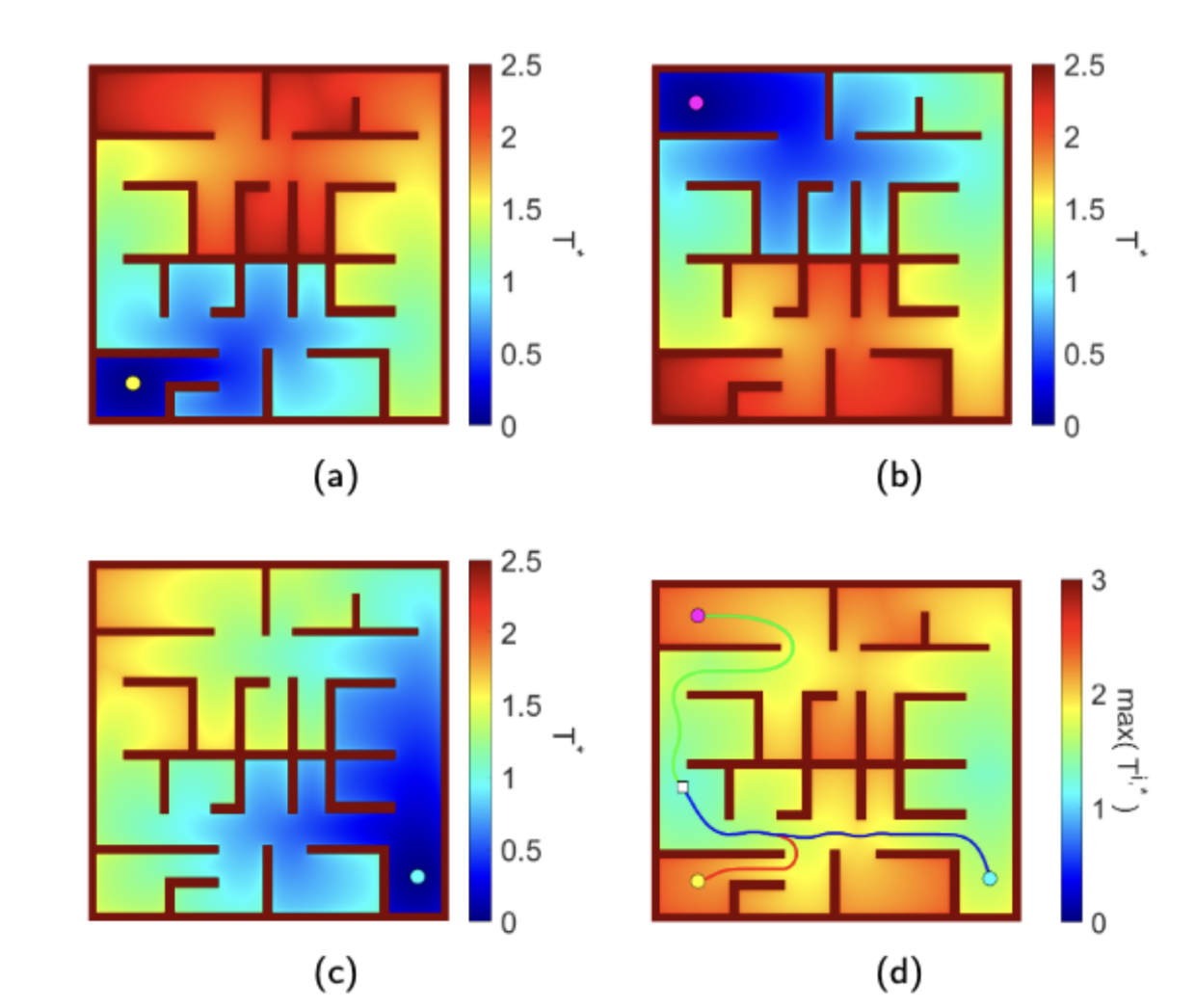
Motion of grain boundaries in polycrystalline materials
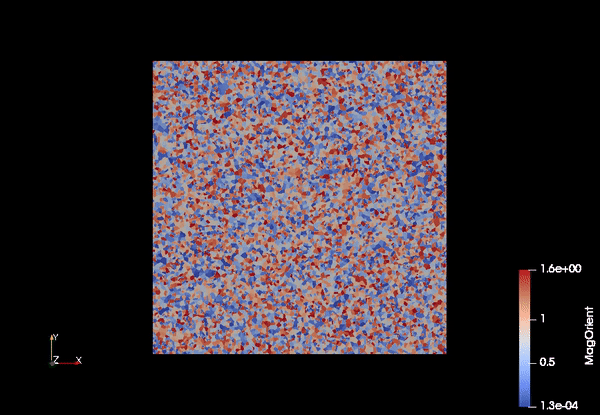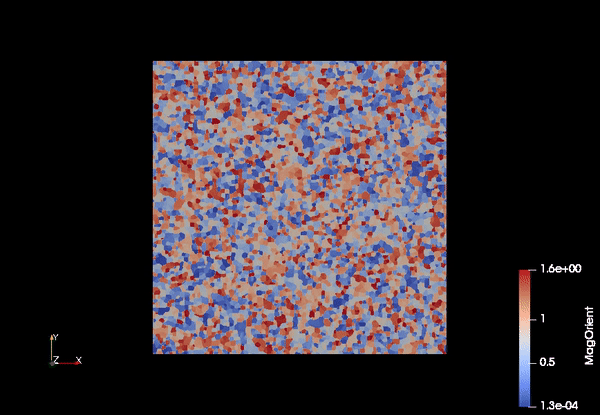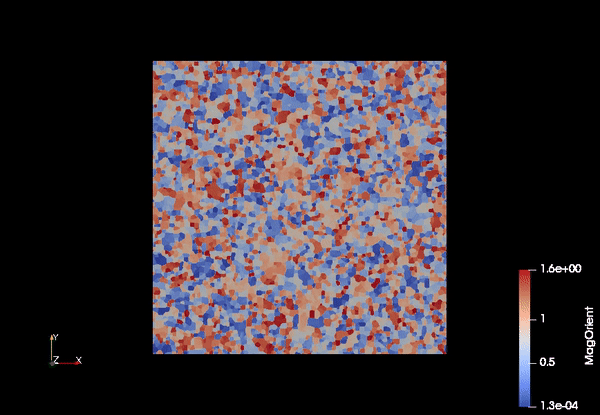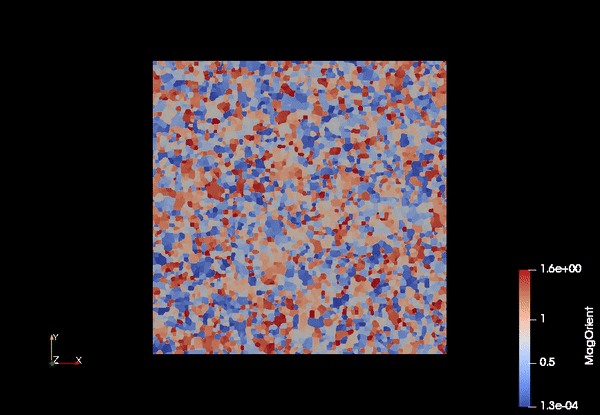
Polyscrystalline materials are composed of many tiny sigle crystal pieces (known as grains) stuck together. It is common microstructure for metals and ceramics. The growth of grain boundaries are of interest because important physical properties (e.g., yield strength, conductivity, etc.) of polycrystalline material depend on the grain boundaries, arising industrial process such as heat treatment (annealing). If one can model and simulate the growth of grainboundaries accurately, polycrystalline materials can be tuned to achieve a variety of uses.
Reduced order modeling using artifical neural network functions

Physically informed neural network (PINN) for non-Newtonian fluid flows
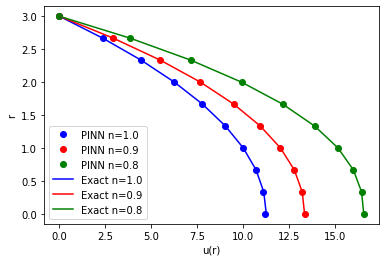
I use machine-learning techniques to solve an elliptic partial differential equation, which typically arises for modeling creeping non-Newtonian fluid flows. In mechanics of non-Newtonian fluid, (often called as computaitonal rheology) the complicated rheological behavior of fluids induces strong non-linearities of the governing equation. Resolving exponential solution profile with a conventional numerical method still remains a challening task. Instead, I take a turn to neural network approach for solving such systems. Rheolgical model provides a vast amount of prior knowledge that may have not been fully exploited. To make the best use of it, physically informed neural network (PINN) transforms clascial mechanic problem into typical minimization problems and train deep neural network to solve supervised learning tasks. This process respects the physics described by constitutive equation of Non-Newtonian models. While the PINN framework is yet premature compared to classcial numerical methods, its potential capability to predict the strong non-linear behavior of a material deserves intensive future research in this field.
Complex fluid flow simulation
I use Finite-element method to simulate non-Newtonian fluid flows. I consider fluid mechanics of rheologically complex fluids with yield stress, viscoelasticity, and thixotropy. While there exist a variety of rheological models to describe these nonlinear fluid-mechanics, parameters of the models are usually fit against data acquired from simplest geometry. Therefore, the uses of rheological models for real material process stage, which often include involved flow geometry, are inherently extrapolative. I consider the uncertainty quantificaiton of such cases and investigate the sensitivity of model parameters in simulation predictions.